CS 116 Tutorial 11 (Solutions): Graph Theory

Reminders:

The Final Exam is on Friday, August 9th, 2019
Assignment 09 is due on Wednesday, July 30th, 2019 at 10:00

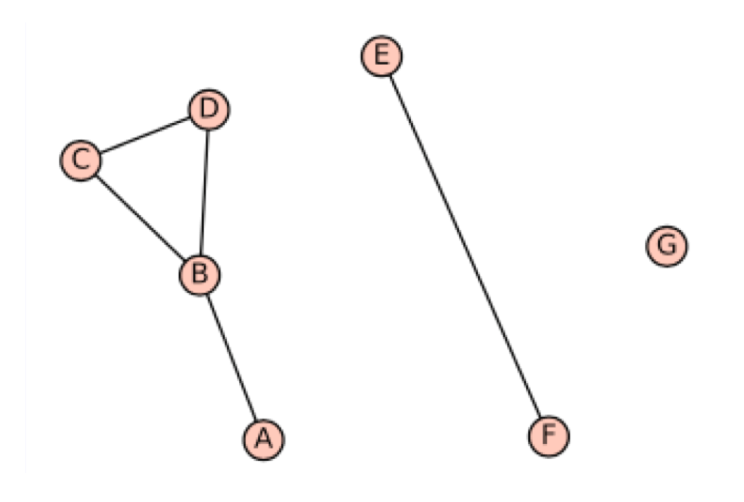
Show how to represent the following graph using:

Edge list representation
Adjacency list representation
Adjacency matrix representation (call 'A' vertex 0, 'B' vertex 1, etc)

Solution: (different order of lists also acceptable)

Edge list:


[['A','B'], ['A','C'],
 ['B','C'], ['B','D'], 
 ['C','E'], ['E','F'],
 ['E','G']]

Adjacency list:


{ 'A':['B','C'], 
  'B':['A','C','D'], 
  'C':['A','B','E'], 
  'D':['B'], 
  'E':['C','F','G'], 
  'F':['E'], 
  'G':['E'] }

Adjacency Matrix:


[ [0,1,1,0,0,0,0], 
  [1,0,1,1,0,0,0], 
  [1,1,0,0,1,0,0], 
  [0,1,0,0,0,0,0], 
  [0,0,1,0,0,1,1], 
  [0,0,0,0,1,0,0], 
  [0,0,0,0,1,0,0] ]

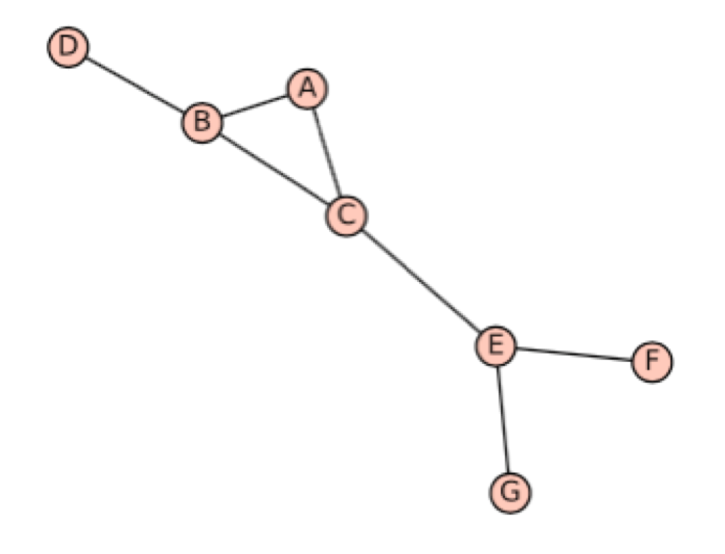
(a) Draw the graph corresponding to the following adjacency list.

{ 'A': ['B', 'C'], 
  'B': ['A', 'D', 'E', 'F'],
  'C': ['A'],
  'D': ['B','E'],
  'E': ['B','D', 'F'],
  'F': ['B','E']}

Solution:

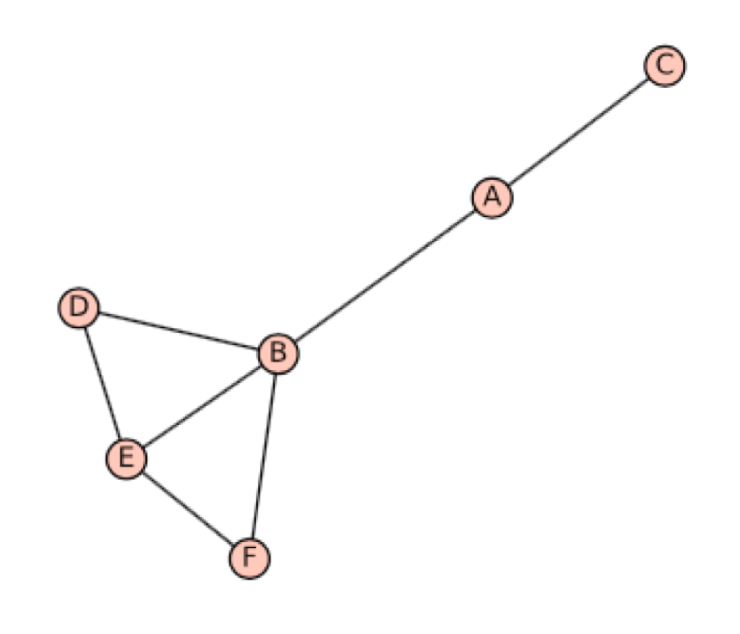
(b) Draw the graph corresponding to the following adjacency matrix.

[[0,1,0,0,0,0,0],
 [1,0,1,1,0,0,0], 
 [0,1,0,1,0,0,0],
 [0,1,1,0,0,0,0],
 [0,0,0,0,0,1,0],
 [0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0]]

(a) Perform bfs and dfs traversals for the following graphs.
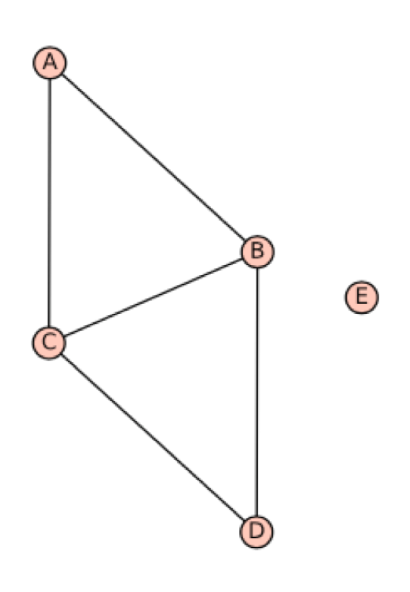
Solution:

Graph 1, starting from A
Example bfs: ABCDEFG, ACBEDGF, ACBEDFG, ABCDEGF
Example dfs: ABDCEFG, ABDCEGF, ACEFGBD, ABCEFGD

Graph 1, starting from E
Example bfs: ECFGABD, EFGCBAD, EGFCABD, EFGCABD
Example dfs: EGFCABD, ECBDAGF, EFCBDAGF, ECABDFG

Graph 2, starting from A
Example bfs: ABCD, ACBD
Example dfs: ACDB, ABDC, ACBD, ABCD

Graph 2, starting from E
Example bfs: E
Example dfs: E

(b) Recursive implementation of dfs traversal.
```
def dfs(graph, v):
    visited = []
    return visit(graph, v, visited)

def visit(g, v, all):
    all.append(v)
    for neighbour in g[v]:
        if neighbour not in all:
            visit(g, neighbour, all)
    return all
```

(a) Write the function vertices_count that consumes a nonempty graph G (stored as an adjacency list) and returns the number of vertices in G.

Solution:

import check

G1={1:[2,5], 2:[1,3], 3:[2], 4:[5], 5:[1,4]}
G2={1:[2,4], 2:[1,3,4,5], 3:[2,5], 4:[1,2], 5:[2,3], 6:[]}
G3={1:[2,3,4], 2:[1,3], 3:[1,2,5], 4:[1,5], 5:[3,4,6], 6:[5]}
G4={}


def vertices_count(G):
    '''
    returns the number of vertices in graph G
    
    count_vertices: (dictof Nat (listof Nat) -> Nat
    requires: Nat > 0
    
    Examples:
    count_vertices(G1) => 5
    count_vertices(G2) => 6
    '''
    return len(G)


# Tests:    
check.expect("T1", vertices_count(G1), 5)
check.expect("T2", vertices_count(G2), 6)
check.expect("T3", vertices_count(G4), 0)

(b) Write the function edges_count that consumes a nonempty graph G (stored as an adjacency list) and returns the number of edges in G.

Solution:

import check

# using constants from Q4a

def edges_count(G):
    '''
    returns the number of edges in graph G
    
    count_vertices: (dictof Nat (listof Nat) -> Nat
    requires: Nat > 0
    
    Examples:
    count_edges(G1) => 5
    count_edges(G2) => 7
    '''
    sume = 0
    for v in G:
        sume += len(G[v])
    return sume // 2
    

# Tests:
check.expect("T1", edges_count(G1), 4)
check.expect("T2", edges_count(G2), 6)
check.expect("T3", edges_count(G3), 7)
check.expect("T4", edges_count(G4), 0)

Solution:

Write the function degree_adj_mat that consumes a nonempty graph G (stored as an adjacency matrix) and a vertex number v, and returns the degree of vertex v in G. Note that the vertices are numbered 0, 1, ..., n-1. G has length n, and each list in G has length n as well.

Challenge Question: On your own, implement the functions degree_adj_list and degree_edges, to determine the degree of a vertex using the other representations.

Solution:

import check

# Adjacency matrix representation - vertices 0,1,2,3,4,5 (slide 13)
g_adj_mat = [ [0,1,0,0,1,0], [1,0,1,0,1,0], [0,1,0,1,0,0],
              [0,0,1,0,1,1], [1,1,0,1,0,0], [0,0,0,1,0,0] ]


def degree_adj_mat(G, v):
    '''
    returns the degree of vertex v in a graph G where G is an adjacency 
    matrix representation of a graph

    degree: (listof (listof Nat)) Nat -> Nat
    requires: 0 < len(G) == len(G[i]) for each i=0:len(G) 
              0 < v < len(G)

    Example: 
    degree([[0]], 0) => 0
    degree(g_adj_mat, 4) => 3
    '''
    row = G[v]
    neighbours = list(filter(lambda e:e==1, row))
    return len(neighbours)

check.expect("degree - 1 vertex, deg 0", degree_adj_mat([[0]], 0), 0)
check.expect("degree - eg - v=0", degree_adj_mat(g_adj_mat, 0), 2)
check.expect("degree - eg - v=1", degree_adj_mat(g_adj_mat, 1), 3)
check.expect("degree - eg - v=2", degree_adj_mat(g_adj_mat, 2), 2)
check.expect("degree - eg - v=3", degree_adj_mat(g_adj_mat, 3), 3)
check.expect("degree - eg - v=4", degree_adj_mat(g_adj_mat, 4), 3)
check.expect("degree - eg - v=5", degree_adj_mat(g_adj_mat, 5), 1)
bigger_g = [ [0,1,0,0,1,0,0], [1,0,1,0,1,0,0], [0,1,0,1,0,0,0],
              [0,0,1,0,1,1,0], [1,1,0,1,0,0,0], [0,0,0,1,0,0,0],
              [0,0,0,0,0,0,0]]
check.expect("bigger graph, degree 0", degree_adj_mat(bigger_g, 6), 0)

Alternate Solution:

def degree_adj_mat(G, v):
    return sum(G[v])

(a) Write the function list_dictionary that consumes a graph G (stored as a dictionary), and returns a list of edges.

Solution:

import check

def list_dictionary(G):
    '''
    return the edge lists to represent G
    
    list_dictionary: (dictof Nat (listof Nat)) -> (listof (listof Nat))
    requires: Nat > 0
    
    Examples:
    list_dictionary({1:[2,5], 2:[1, 3, 5], 3:[2, 4], 4:[3, 5, 6], 5:[1, 2, 4], \
    6:[4]}) => [[1, 2], [1, 5], [2, 3], [2, 5], [3, 4], [4, 5], [4, 6]]
    list_dictionary({1:[2, 3], 2:[1], 3:[1]}) => [[1, 2], [1, 3]]
    
    '''
    
    l = []
    for key in G:
        for item in G[key]:
            if ([key, item] not in l) and ([item, key] not in l):
                l.append([key, item])
    return l
    
check.expect('t1', list_dictionary({1:[2,5], 2:[1, 3, 5], 3:[2, 4], \
                                    4:[3, 5, 6], 5:[1, 2, 4], 6:[4]}), \
            [[1, 2], [1, 5], [2, 3], [2, 5], [3, 4], [4, 5], [4, 6]])
check.expect('t2', list_dictionary({1:[2, 3], 2:[1], 3:[1]}), [[1, 2], [1, 3]])

(b) Write the function admatrix_dictionary that consumes a graph G (stored as a dictionary), and returns the graph which is stored as a adjacency matrix.

Solution:

import check

def admatrix_dictionary(G):
    '''
    
    return the adjacency matrix that represent G
    
    admatrix_dictionary: (dictof Nat (listof Nat)) -> (listof (listof Nat))
    requires: Nat > 0
    
    Examples:
    admatrix_dictionary({1:[2,5], 2:[1, 3, 5], 3:[2, 4], 4:[3, 5, 6], 5:[1, 2, 4], \
    6:[4]}) => [[0,1,0,0,1,0], [1,0,1,0,1,0], [0,1,0,1,0,0], [0,0,1,0,1,1],\
    [1,1,0,1,0,0], [0,0,0,1,0,0]]
    admatrix_dictionary({1:[2, 3], 2:[1], 3:[1]}) => [[0,1,1], [1,0,0], [1,0,0]]
    '''
    
    l = []
    length = len(G.keys())
    for i in range(length):
        l.append([])
    for lst in l:
        for k in range(length):
            l[k].append(0)
    for key in G:
        for neighbour in G[key]:
            l[key-1][neighbour-1] += 1
            
    return l
    
check.expect('t1', admatrix_dictionary({1:[2,5], 2:[1, 3, 5], 3:[2, 4], \
                                        4:[3, 5, 6], 5:[1, 2, 4],  6:[4]}), \
             [[0,1,0,0,1,0], [1,0,1,0,1,0], [0,1,0,1,0,0], [0,0,1,0,1,1],\
                 [1,1,0,1,0,0], [0,0,0,1,0,0]])
check.expect('t2', admatrix_dictionary({1:[2, 3], 2:[1], 3:[1]}), \
             [[0,1,1], [1,0,0], [1,0,0]])

CS 116: Introduction to Computer Science 2

CS 116 Tutorial 11 (Solutions): Graph Theory

Reminders: